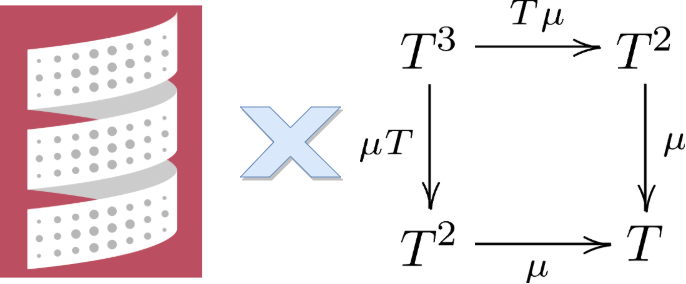Scalaプログラマが圏論を学ぶためのオススメ文献 - 3選

圏論は数学の一分野です。これを学ぶのには「数学書」を手に取るのが王道なのですが、残念ながらこれは大部分のプログラマに理解できる言葉では書かれていません。「定義・命題・証明」の積み重ねで書かれています^1。ここで大半のScalaプログラマは苦い顔をすると思います。もう少し分かりやすいScalaプログラマ向けの圏論入門がないかと探してみると「Haskell」向けの記事が大量に引っかかるでしょう。ここで多くのScalaプログラマは心を折られてしまいます。「圏論」はまだScalaプログラマには早すぎたんだと・・・ 本記事ではそんなあなたに贈る3つの文献をご紹介したいと思います。
はじめに
本記事は圏論に興味があるScalaプログラマを対象にしています。特にプログラマにとって実用的な圏論の知識をScalaを通して身につけたい方にオススメします。
プログラマが圏論を学ぶべき理由
プログラマが圏論を学ぶべき理由に関しては圏論入門レベルの自分があまり大きなことは言えないので、「Category Theory for Programmers Scala Edition」の序文から3つの文章を引用しようと思います。
First, category theory is a treasure trove of extremely useful programming ideas.
(意訳) 最初に、圏論はめちゃくちゃ役立つプログラミングのアイデアの宝庫です。
I would go as far as to argue that category theory is the kind of math that is particularly well suited for the minds of programmers.That’s because category theory — rather than dealing with particulars — deals with structure. It deals with the kind of structure that makes programs composable.
(意訳) 圏論はプログラマの心理に特に適した数学の分野であるといっても過言ではないと思います。それは圏論が個々の詳細よりもむしろ構造を扱うからです。圏論はプログラムを合成可能にする特定の構造を扱います。
Composition is at the very root of category theory — it’s part of the definition of the category itself. And I will argue strongly that composition is the essence of programming.
(意訳) 合成は圏論の重要な根幹を成しており、圏自体の定義の一部でもあります。そして合成はプログラミングの本質であると、はっきり述べておこうと思います。
オンラインで読めるオススメ文献 - 3選
本記事は「Scalaプログラマに適した圏論の文献紹介」という趣旨なので、以下の条件に当てはまる文献を3つに絞って紹介したいと思います。
- 圏論の概念(特にモノイド、関手、モナド)に触れている
- Scalaで解説がしてある
- 定理の証明が極力載っていない
- オンラインで無料で読める
Category Theory for Programmers Scala Edition
まずは前述した「Category Theory for Programmers Scala Edition」を紹介します。
- Category Theory for Programmers: The Preface | Bartosz Milewski's Programming Cafe
- 元のHaskellで書かれたページ
- Category Theory for Programmers Scala Edition
- Scalaエディションのダウンロードページ
- 上記のページから「category-theory-for-programmers-scala.pdf」をダウンロード
この本はもともとHaskell(と若干のC++)で書かれていた例に、後でScalaの例を付け加えたものになっています。この本の特徴のひとつは豊富な図解とスニペットです。これは具体的に引用して見てもらった方が早いと思います。以下は10章の自然変換で使われている4つの図になります。
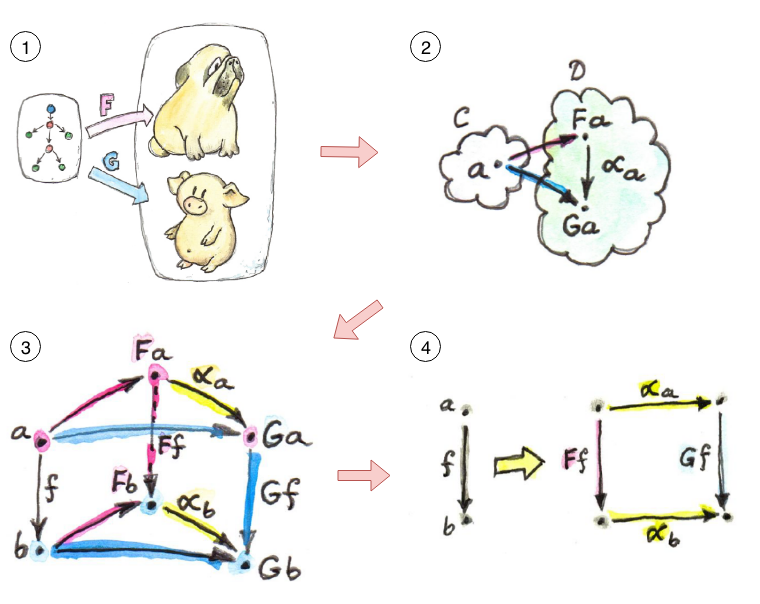
番号と赤い矢印は自分が書き足したものです。一般の数学書による自然変換の説明だと最後の4番目の図のしかも右側の可換図式しか描かれていない場合がほとんどだと思います。しかし本書では1番目の図で同じ圏に移す2つの関手FとGが示されて図式が犬と豚に変換されているイメージが描かれています。2番目の図では、自然変換が対象を移すことを示し、3番目の図で対象だけでなく射も移すことを示しています。そして3番目を簡略化したものが4番目の図になることが分かります^2。
このように本書では圏論の概念が豊富な図によって解説されています。またソースコードもHaskellとScalaのコードが一緒に載っていて非常にわかりやすいです。以下の引用はListの長さを示すlength関数が自然変換であることの説明に使われているコードです。

length関数は一般的にはList[A] => Intの関数でList関手をIntに変換するものですが、Intを定値関手であるConst[E, A]に埋め込まれたConst[Int, A]と見做すことでlengthを関手間の変換、つまり自然変換になることを示しています。本書では関手間のパラメトリックな多相関数は常に自然変換になることを述べています。
上記のように本書では一貫してHaskellのコードが青、Scalaのコードが赤で示されており非常にわかりやすくなっています。一般的な圏論のプログラミングへの応用ではHaskellを例に出されることが多いので、このように併記してある文献はHaskellを学びたいScalaプログラマにとっても嬉しいと思われます。
最後に本書の内容と構成に関してですが、自分は圏論を学びたいプログラマにとっては非常に秀逸だと思いました。少なくとも数学にはあまり自身がないけどプログラミングに圏論を活かしたいプログラマにとっては必要な概念はほぼ本書で触れられていると思います。
以下に本書の目次(一部抜粋)を載せておきます^3。また、自分の日本語訳とプログラマとして読んだ方がいい章を5段階評価で★印を付けています。本書を読む参考にしてください。
目次(日本語訳付き)
- Preface (序文) ★★★★★
- 1 Category: The Essence of Composition (圏: 合成の本質) ★★★★★
- 1.1 Arrows as Functions (関数としての矢)
- 1.2 Properties of Composition (合成の性質)
- 1.3 Composition is the Essence of Programming (合成はプログラミングの本質)
- 2 Types and Functions (型と関数) ★★★★
- 2.1 Who Needs Types? (なぜ型が必要なのか?)
- 2.2 Types Are About Composability (型は合成可能性に関係する)
- 2.3 What Are Types? (型とは何か?)
- 2.4 Why Do We Need a Mathematical Model? (なぜ数学モデルが必要なのか?)
- 2.5 Pure and Dirty Functions (純粋な関数と汚れた関数)
- 2.6 Examples of Types (型の例)
- 3 Categories Great and Small (圏 大から小まで) ★★
- 3.1 No Objects (対象なし)
- 3.2 Simple Graphs (単純なグラフ)
- 3.3 Orders (順序)
- 3.4 Monoid as Set (集合としてのモノイド)
- 3.5 Monoid as Category (圏としてのモノイド)
- 4 Kleisli Categories (クライスリ圏) ★★★
- 4.1 The Writer Category (
Writerの圏) - 4.2 Writer in Haskell (Haskellにおける
Writer) - 4.3 Kleisli Categories (クライスリ圏)
- 4.1 The Writer Category (
- 5 Products and Coproducts (積と余積) ★★★
- 5.1 Initial Object (始対象)
- 5.2 Terminal Object (終対象)
- 5.3 Duality (双対)
- 5.4 Isomorphisms (同型)
- 5.5 Products (積)
- 5.6 Coproduct (余積)
- 5.7 Asymmetry (非対称)
- 6 Simple Algebraic Data Types (単純な代数的データ型) ★★★
- 6.1 Product Types (積型)
- 6.2 Records (レコード型)
- 6.3 Sum Types (和型)
- 6.4 Algebra of Types (型の代数)
- 7 Functors (関手) ★★★★
- 7.1 Functors in Programming (プログラミングにおける関手)
- 7.1.1 The Maybe Functor (
Maybe関手) - 7.1.2 Equational Reasoning (等式的推論)
- 7.1.3 Optional (
Optional) - 7.1.4 Typeclasses (型クラス)
- 7.1.5 Functor in C++ (C++における関手)
- 7.1.6 The List Functor (
List関手) - 7.1.7 The Reader Functor (
Reader関手)
- 7.1.1 The Maybe Functor (
- 7.2 Functors as Containers (コンテナとしての関手)
- 7.3 Functor Composition (関手の合成)
- 7.1 Functors in Programming (プログラミングにおける関手)
- 8 Functoriality (関手っぽいもの) ★★
- 8.1 Bifunctors (双関手)
- 8.2 Product and Coproduct Bifunctors (積と余積双関手)
- 8.3 Functorial Algebraic Data Types (関手的代数的データ型)
- 8.4 Functors in C++ (C++における関手)
- 8.5 The Writer Functor (
Writer関手) - 8.6 Covariant and Contravariant Functors (共変と反変関手)
- 8.7 Profunctors (プロ関手)
- 8.8 The Hom-Functor (ホム関手)
- 9 Function Types (関数型) ★★★★
- 9.1 Universal Construction (普遍的構成)
- 9.2 Currying (カリー化)
- 9.3 Exponentials (冪)
- 9.4 Cartesian Closed Categories (デカルト閉圏/カルテシアン閉圏)
- 9.5 Exponentials and Algebraic Data Types (冪と代数的データ型)
- 9.5.1 Zeroth Power (0乗)
- 9.5.2 Powers of One (1の冪乗)
- 9.5.3 First Power (1乗)
- 9.5.4 Exponentials of Sums (和の指数)
- 9.5.5 Exponentials of Exponentials (冪の指数)
- 9.5.6 Exponentials over Products (積の指数)
- 9.6 Curry-Howard Isomorphism (カリー・ハワード同型)
- 10 Natural Transformations (自然変換) ★★★
- 10.1 Polymorphic Functions (多相関数)
- 10.2 Beyond Naturality (自然性を超えて)
- 10.3 Functor Category (関手圏)
- 10.4 2-Categories (2圏)
- 11 Declarative Programming (宣言的プログラミング) ★★
- 12 Limits and Colimits (極限と余極限) ★★
- 12.1 Limit as a Natural Isomorphism (極限と自然同型)
- 12.2 Examples of Limits (極限の例)
- 12.3 Colimits (余極限)
- 12.4 Continuity (連続性)
- 13 Free Monoids (自由モナド) ★★★
- 13.1 Free Monoid in Haskell (Haskellにおける自由モノイド)
- 13.2 Free Monoid Universal Construction (自由モノイドの普遍的構成)
- 14 Representable Functors (表現可能関手) ★★
- 14.1 The Hom Functor (ホム関手)
- 14.2 Representable Functors (表現可能関手)
- 15 The Yoneda Lemma (米田の補題) ★★
- 15.1 Yoneda in Haskell (Haskellにおける米田)
- 15.2 Co-Yoneda (余米田)
- 16 Yoneda Embedding (米田埋め込み) ★★
- 16.1 The Embedding (埋め込み)
- 16.2 Application to Haskell (Haskellへの応用)
- 16.3 Preorder Example (前順序の例)
- 16.4 Naturality (自然性)
- 17 It’s All About Morphisms (結局は射が全て) ★★★
- 17.1 Functors (関手)
- 17.2 Commuting Diagrams (可換図式)
- 17.3 Natural Transformations (自然変換)
- 17.4 Natural Isomorphisms (自然同型)
- 17.5 Hom-Sets (ホム集合)
- 17.6 Hom-Set Isomorphisms (ホム集合同型)
- 17.7 Asymmetry of Hom-Sets (ホム集合の非対称)
- 18 Adjunctions (随伴) ★★
- 18.1 Adjunction and Unit/Counit Pair (随伴と単位/余単位)
- 18.2 Adjunctions and Hom-Sets (随伴とホム集合)
- 18.3 Product from Adjunction (随伴から積へ)
- 18.4 Exponential from Adjunction (随伴から冪へ)
- 19 Free/Forgetful Adjunctions (自由/忘却随伴) ★★
- 20 Monads: Programmer’s Definition (モナド: プログラマーの定義) ★★★★
- 20.1 The Kleisli Category (クライスリ圏)
- 20.2 Fish Anatomy (魚の解剖学)
- 20.3 The do Notation (
do記法)
- 21 Monads and Effects (モナドと作用) ★★★
- 21.1 The Problem (問題)
- 21.2 The Solution (解決策)
- 21.2.1 Partiality (部分性)
- 21.2.2 Nondeterminism (非決定性)
- 21.2.3 Read-Only State (読み取りのみの状態)
- 21.2.4 Write-Only State (書き取りのみの状態)
- 21.2.5 State (状態)
- 21.2.6 Exceptions (例外)
- 21.2.7 Continuations (継続)
- 21.2.8 Interactive Input (対話型の入力)
- 21.2.9 Interactive Output (対話型の出力)
- 22 Monads Categorically (圏論的なモナド) ★★
- 22.1 Monoidal Categories (モノイダル圏)
- 22.2 Monoid in a Monoidal Category (モノイダル圏におけるモノイド)
- 22.3 Monads as Monoids (モノイドとしてのモナド)
- 22.4 Monads from Adjunctions (随伴としてのモナド)
- 23 Comonads (余モナド) ★
- 23.1 Programming with Comonads (余モナドでプログラミング)
- 23.2 The Product Comonad (積余モナド)
- 23.3 Dissecting the Composition (合成の解剖)
- 23.4 The Stream Comonad (ストリーム余モナド)
- 23.5 Comonad Categorically (圏論的な余モナド)
- 23.6 The Store Comonad (ストア余モナド)
- 24 F-Algebras (F代数) ★★★
- 24.1 Recursion (再帰)
- 24.2 Category of F-Algebras (F代数の圏)
- 24.3 Natural Numbers (自然数)
- 24.4 Catamorphisms (カタモーフィズム)
- 24.5 Folds (畳み込み)
- 24.6 Coalgebras (余代数)
- 25 Algebras for Monads (モナドの代数) ★★
- 25.1 T-algebras (T代数)
- 25.2 The Kleisli Category (クライスリ圏)
- 25.3 Coalgebras for Comonads (余モナドの余代数)
- 25.4 Lenses (レンズ)
- 26 Ends and Coends (エンドと余エンド) ★
- 26.1 Dinatural Transformations (対角化自然変換)
- 26.2 Ends (エンド)
- 26.3 Ends as Equalizers (等価子としてのエンド)
- 26.4 Natural Transformations as Ends (エンドとしての自然変換)
- 26.5 Coends (余エンド)
- 26.6 Ninja Yoneda Lemma (忍者米田の補題)
- 26.7 Profunctor Composition (プロ関手の合成)
- 27 Kan Extensions (カン拡張) ★
- 27.1 Right Kan Extension (右カン拡張)
- 27.2 Kan Extension as Adjunction (随伴としてのカン拡張)
- 27.3 Left Kan Extension (左カン拡張)
- 27.4 Kan Extensions as Ends (エンドとしてのカン拡張)
- 27.5 Kan Extensions in Haskell (Haskellにおけるカン拡張)
- 27.6 Free Functor (自由関手)
- 28 Enriched Categories (豊穣圏) ★
- 28.1 Why Monoidal Category? (なぜ豊穣圏なのか?)
- 28.2 Monoidal Category (モノイダル圏)
- 28.3 Enriched Category (豊穣圏)
- 28.4 Preorders (前順序)
- 28.5 Metric Spaces (距離空間)
- 28.6 Enriched Functors (豊穣関手)
- 28.7 Self Enrichment (自己豊穣化)
- 28.8 Relation to 𝟐-Categories (2圏との関係)
- 29 Topoi (トポス) ★
- 29.1 Subobject Classifier (部分対象分類子)
- 29.2 Topos (トポス)
- 29.3 Topoi and Logic (トポスと論理)
- 30 Lawvere Theories (ローヴェア理論) ★
- 30.1 Universal Algebra (普遍代数)
- 30.2 Lawvere Theories (ローヴェア理論)
- 30.3 Models of Lawvere Theories (ローヴェア理論のモデル)
- 30.4 The Theory of Monoids (モノイドの理論)
- 30.5 Lawvere Theories and Monads (ローヴェア理論とモナド)
- 30.6 Monads as Coends (余エンドとしてのモナド)
- 30.7 Lawvere Theory of Side Effects(副作用のローヴェア理論)
- 31 Monads, Monoids, and Categories (モナドとモノイドと圏) ★★
- 31.1 Bicategories (双圏)
- 31.2 Monads (モナド)
Scala with Cats
次に紹介したいのは「Scala with Cats」です[^4]。CatsはScalaで関数型プログラミングをサポートするためのライブラリで、主に型クラスを提供しています。この型クラスにはモナド(Monad)や関手(Functor)も含まれており、圏論をプログラミングに応用する上で重要な役割を果たしています。
この本の特色は「型チャート」が豊富に載っていることです。Scalaの型は圏論においては対象や関手やモナドだったり様々ですが、それらの変換の様子が図に表されているので非常に分かりやすくなっています。以下の引用は反変関手の型チャートになります。
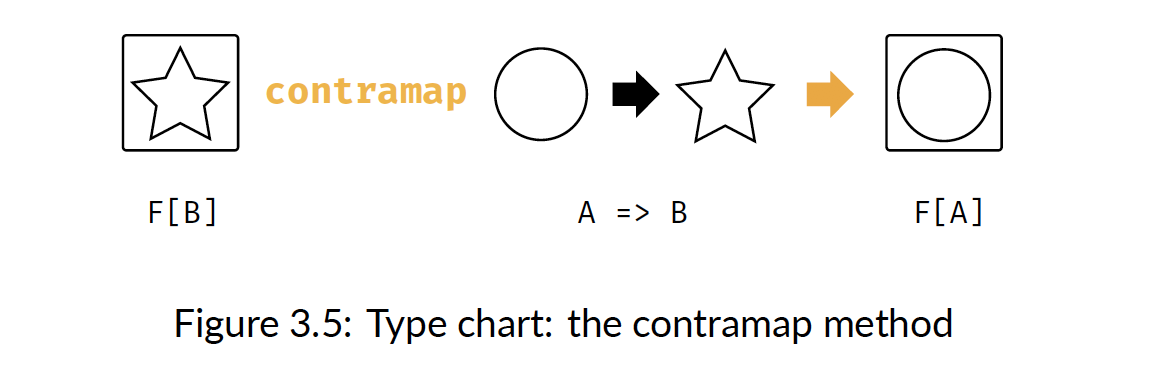
本書の構成で秀逸なのは、型クラスの説明に留まらず「Case Study(事例)」と「Solution(答え)」が載っていることです。Case Studyには、具体的のどのようなケースで型クラスを使えばいいかが載っています。「Solution」には、各章に豊富に散りばめられた「Excercise」の答えが載っています。従って本書を読むことで圏論の一部を「実務」でも応用できるようになると思います。
以下に本書の目次(一部抜粋)を載せておきます[^5]。また、自分の日本語訳付けていますが・・・途中で力尽きました。本書を読む参考にしてください。
[^4]: この本はもともと「Scalaz」という別のライブラリ向けに書かれていたものが、Cats向けに書き直されたものです。書き直された当初は「Advanced Scala with Cats」という名前で有償でしたが、無償化されるにあたって「Scala with Cats」という名称に変更され可愛らしい猫の表紙が付きました。
[^5]: 掲載している目次は、「Summary」、「Excercise」、「Solution」等の見出しは削っております。これは本書の概要を知る手がかりにはならないと考えたからです。正しい目次は直接文献をご確認ください。
目次(日本語訳付き)
- 1 Introduction (はじめに)
- 1.1 Anatomy of a Type Class (型クラスの解剖学)
- 1.1.1 The Type Class (型クラス)
- 1.1.2 Type Class Instances (型クラスインスタンス)
- 1.1.3 Type Class Interfaces (型クラスインタフェース)
- 1.2 Working with Implicits (暗黙と働く)
- 1.2.1 Packaging Implicits (暗黙のパッケージ)
- 1.2.2 Implicit Scope (暗黙のスコープ)
- 1.2.3 Recursive Implicit Resolution (再帰的な暗黙の解決)
- 1.3 Exercise: Printable Library (練習: 印字可能ライブラリ)
- 1.4 Meet Cats (Catsとの邂逅)
- 1.4.1 Importing Type Classes (型クラスのインポート)
- 1.4.2 Importing Default Instances (デフォルトインスタンスのインポート)
- 1.4.3 Importing Interface Syntax (インタフェース構文のインポート)
- 1.4.4 Importing All The Things! (全てをインポート!)
- 1.4.5 Defining Custom Instances (カスタムインスタンスを定義する)
- 1.5 Example: Eq (例:
Eq)- 1.5.1 Equality, Liberty, and Fraternity (等値性、自由、友愛)
- 1.5.2 Comparing Ints (
Intの比較) - 1.5.3 Comparing Options (
Optionの比較) - 1.5.4 Comparing Custom Types (カスタム型の比較)
- 1.6 Controlling Instance Selection (インスタンス選択の制御)
- 1.6.1 Variance (変位)
- 1.1 Anatomy of a Type Class (型クラスの解剖学)
- 2 Monoids and Semigroups (モノイドと半群)
- 2.1 Definition of a Monoid (モノイドの定義)
- 2.2 Definition of a Semigroup (半群の定義)
- 2.3 Exercise: The Truth About Monoids (モナドの真実)
- 2.4 Exercise: All Set for Monoids (モノイドの全ての集合)
- 2.5 Monoids in Cats (Catsにおけるモノイド)
- 2.5.1 The Monoid Type Class (モノイド型クラス)
- 2.5.2 Monoid Instances (モノイドインタンス)
- 2.5.3 Monoid Syntax (モノイド構文)
- 2.6 Applications of Monoids (モノイドの応用)
- 2.6.1 Big Data (ビッグデータ)
- 2.6.2 Distributed Systems (分散システム)
- 2.6.3 Monoids in the Small (小さな世界におけるモノイド)
- 3 Functors (関手)
- 3.1 Examples of Functors (関手の例)
- 3.2 More Examples of Functors (関手のさらなる例)
- 3.3 Definition of a Functor (関手の定義)
- 3.4 Aside: Higher Kinds and Type Constructors (寄り道: 高カインドと型コンストラクタ)
- 3.5 Functors in Cats (Catsにおける関手)
- 3.5.1 The Functor Type Class (関手型クラス)
- 3.5.2 Functor Syntax (関手構文)
- 3.5.3 Instances for Custom Types (カスタム型のインスタンス)
- 3.6 Contravariant and Invariant Functors (反変・不変関手)
- 3.6.1 Contravariant Functors and the contramap Method (反変関手と
contramapメソッド) - 3.6.2 Invariant functors and the imap method(不変関手と
imap)
- 3.6.1 Contravariant Functors and the contramap Method (反変関手と
- 3.7 Contravariant and Invariant in Cats (Catsにおける
ContravariantとInvariant)- 3.7.1 Contravariant in Cats (Catsにおける
Contravariant) - 3.7.2 Invariant in Cats (Catsにおける
Invariant)
- 3.7.1 Contravariant in Cats (Catsにおける
- 3.8 Aside: Partial Unification (寄り道: 部分的ユニフィケーション)
- 3.8.1 Unifying Type Constructors (型コンストラクタの結合)
- 3.8.2 Left-to-Right Elimination (左から右への削除)
- 4 Monads (モナド)
- 4.1 What is a Monad? (モナドとは何か)
- 4.1.1 Definition of a Monad (モナドの定義)
- 4.2 Monads in Cats (Catsにおけるモナド)
- 4.2.1 The Monad Type Class(モナド型クラス)
- 4.2.2 Default Instances(デフォルトインスタンス)
- 4.2.3 Monad Syntax(モナド構文)
- 4.3 The Identity Monad(恒等モナド)
- 4.4 Either (
Either)- 4.4.1 Left and Right Bias (左右バイアス)
- 4.4.2 Creating Instances (インスタンスの作成)
- 4.4.3 Transforming Eithers (
Eitherへの変換) - 4.4.4 Error Handling (エラーハンドリング)
- 4.5 Aside: Error Handling and MonadError (寄り道: エラーハンドリングと
MonadError)- 4.5.1 The MonadError Type Class (
MonadError型クラス) - 4.5.2 Raising and Handling Errors (エラーの投げ方とハンドリングの仕方)
- 4.5.3 Instances of MonadError (
MonadErrorのインスタンス)
- 4.5.1 The MonadError Type Class (
- 4.6 The Eval Monad (
Evalモナド)- 4.6.1 Eager, Lazy, Memoized, Oh My! (熱心、怠惰、メモ化、オッ!)
- 4.6.2 Eval’s Models of Evaluation (
Evalの評価モデル) - 4.6.3 Eval as a Monad (モナドとしての
Eval) - 4.6.4 Trampolining and Eval.defer (トランポリンと
Eval.defer)
- 4.7 The Writer Monad (
Writerモナド)- 4.7.1 Creating and Unpacking Writers (
Writerの作成と開封) - 4.7.2 Composing and Transforming Writers ((
Writerの合成と変換))
- 4.7.1 Creating and Unpacking Writers (
- 4.8 The Reader Monad (
Readerモナド)- 4.8.1 Creating and Unpacking Readers (
Readerの作成と開封) - 4.8.2 Composing Readers (
Readerの合成) - 4.8.3 Exercise: Hacking on Readers (練習:
Readerでハッキング) - 4.8.4 When to Use Readers? (いつ
Readerを使うか?)
- 4.8.1 Creating and Unpacking Readers (
- 4.9 The State Monad (
Stateモナド)- 4.9.1 Creating and Unpacking State (
Stateの作成と開封) - 4.9.2 Composing and Transforming State (
Stateの合成と変換)
- 4.9.1 Creating and Unpacking State (
- 4.10 Defining Custom Monads (カスタムモナドの定義)
- 4.1 What is a Monad? (モナドとは何か)
- 5 Monad Transformers (モナド変換子)
- 5.1 Exercise: Composing Monads (練習: モナドの合成)
- 5.2 A Transformative Example (変換的な例)
- 5.3 Monad Transformers in Cats (Catsにおけるモナド変換子)
- 5.3.1 The Monad Transformer Classes (モナド変換子クラス)
- 5.3.2 Building Monad Stacks (モナドスタックの構築)
- 5.3.3 Constructing and Unpacking Instances (インスタンスの構成と開封)
- 5.3.4 Default Instances (デフォルトインスタンス)
- 5.3.5 Usage Patterns (利用パターン)
- 6 Semigroupal and Applicative (半群とアプリカティブ)
- 6.1 Semigroupal (
Semigroupal)- 6.1.1 Joining Two Contexts (2つのコンテキストの結合)
- 6.1.2 Joining Three or More Contexts (3つ以上のコンテキストの結合)
- 6.2 Apply Syntax (
Apply構文) - 6.2.1 Fancy Functors and Apply Syntax (面白い
FunctorとApply構文) - 6.3 Semigroupal Applied to Different Types (
Semigroupalの異なる型への適用)- 6.3.1 Semigroupal Applied to Monads (
Semigroupalのモナドへの適用)
- 6.3.1 Semigroupal Applied to Monads (
- 6.4 Validated (
Validated)- 6.4.1 Creating Instances of Validated (
Validatedのインスタンス作成) - 6.4.2 Combining Instances of Validated (
Validatedのインスタンス結合) - 6.4.3 Methods of Validated (
Validatedのメソッド)
- 6.4.1 Creating Instances of Validated (
- 6.5 Apply and Applicative (
ApplyとApplicative)- 6.5.1 The Hierarchy of Sequencing Type Classes (列型クラスの階層)
- 6.1 Semigroupal (
- 7 Foldable and Traverse (
FoldableとTraverse)- 7.1 Foldable (
Foldable)- 7.1.1 Folds and Folding
- 7.1.2 Exercise: Reflecting on Folds
- 7.1.3 Exercise: Scaf-fold-ing Other Methods
- 7.1.4 Foldable in Cats
- 7.2 Traverse
- 7.2.1 Traversing with Futures
- 7.2.2 Traversing with Applicatives
- 7.2.3 Traverse in Cats
- 7.1 Foldable (
- 8 Case Study: Testing Asynchronous Code (事例: 非同期コードのテスト)
- 8.1 Abstracting over Type Constructors
- 8.2 Abstracting over Monads
- 9 Case Study: Map-Reduce (事例: Map-Reduce)
- 9.1 Parallelizing map and fold
- 9.2 Implementing foldMap
- 9.3 Parallelising foldMap
- 9.3.1 Futures, Thread Pools, and ExecuonContexts
- 9.3.2 Dividing Work
- 9.3.3 Implementing parallelFoldMap
- 9.3.4 parallelFoldMap with more Cats
- 10 Case Study: Data Validation (事例: データバリデーション)
- 10.1 Sketching the Library Structure
- 10.2 The Check Datatype
- 10.3 Basic Combinators
- 10.4 Transforming Data
- 10.4.1 Predicates
- 10.4.2 Checks
- 10.5 Kleislis
- 11 Case Study: CRDTs (事例: CRDT)
- 11.1 Eventual Consistency
- 11.2 The GCounter
- 11.2.1 Simple Counters
- 11.2.2 GCounters
- 11.3 Generalisation
- 11.3.1 Implementation
- 11.4 Abstracting GCounter to a Type Class
- 11.5 Abstracting a Key Value Store
猫番
最後に紹介したいのが「猫番」です。紹介する中では唯一の日本語で読める文献です。現在は「O日目」から「17日目」まで公開されており、著者が「Cats」を使って理解していく過程が記録されています。後半はより「圏論」の説明に移っています。
「猫番」は前二つの文献と比べ非常に自由に書かれていて、独特な構成になっています。ただそれが不思議と読みにくいという訳でもなく、著者と一緒に「Cats」や「圏論」を旅をしている気分になれるところがこの文献の面白いところです。もっと気楽に圏論に触れてみたい人や圏論の雰囲気を味わってみたい方はこの文献から読むといいかもしれません。
プログラマが圏論で学んでおいたほうがよい概念
とりあえず「Category Theory for Programmers Scala Edition」に出てきた概念の中で、プログラマが学んでおいた方が良いと思うものを以下に分類してみました^6。これはあくまで数学が苦手な圏論入門者である自分の私見です。
- 必ず学んでおきたい
- 圏、関手、自然変換
- 集合の圏(Set)、圏の圏(Cat)、関手圏
- 半群、モノイド
- モナド、クライスリ圏
- 普遍的構成(普遍性)
- できれば学んでおきたい
- 積、余積
- 同型
- 双対
- 冪、デカルト閉圏
- モノイダル圏
- 自由モノイド、自由モナド
- F代数、T代数
- 余力があれば学んでおきたい
- ホム関手、表現可能関手
- 米田の補題、米田埋め込み
- 極限と余極限
- 随伴
- カリー=ハワード同型
- 興味があれば学んだ方が良い
- エンド
- カン拡張 ←
全ての概念 - 豊穣圏
- トポス
- ローヴェア理論
圏論は非常に多くの概念が出てくるので無理せず少しずつ消化していくのが良いと思われます。自分が圏論に興味を持ち始めたのは「モナド」に出会ってからでした。以下の言葉の意味を知りたくて圏論を始めたのがきっかけです。
モナドは単なる自己関手の圏におけるモノイド対象だよ。何か問題でも?
この言葉の意味は恐らく「必ず学んでおきたい」まで理解できればなんとなく意味が理解できるようになると思われます。さらに圏論にはパワーワード「全ての概念はKan拡張である」[^7]があって、いつか理解できればいいなと思っています。
[^7]: 参考文献: 全ての概念はKan拡張である、とは何か - algebraic dialy | 壱大整域
まとめ
本記事ではプログラマがなぜ圏論を学ぶべきかを説明し、Scalaプログラマが圏論を学ぶ上で有用な以下の3つの文献を紹介しました。
本記事がScalaで圏論を学んでみたい方の一助になれば幸いです。
もっと圏論を学びたい人向けのオンラインで読めるオススメ資料
残念ながら本記事の趣旨には合いませんでしたが、プログラマが圏論を学ぶ上でぜひオススメしたい資料です。
- プログラマーのための圏論
- 物理学者のための圏論入門
- 物理学者ではなくても圏論の基本的な概念を理解できる非常にオススメの資料です
- 特に
普遍射の説明が秀逸で、会社組織に擬えての説明がツボりました
- 圏論によるプログラミングと論理
- 灘校パソコン研究部の部誌(2013年)に掲載されていたものです
- 普通に書店に並んでいてもおかしくないボリュームとクオリティです
- 圏論だけでなく数学やコンピュータサイエンスの基礎も補完しています
- 圏論 | 壱大整域
- 圏論の概念を本気で理解したくなったらここに駆け込んでください
- ただしストイックな数学スタイルで書かれているのでプログラマには少し辛いかもしれません