Scala3と圏論とプログラミング

2020-02-11Tech / Language,

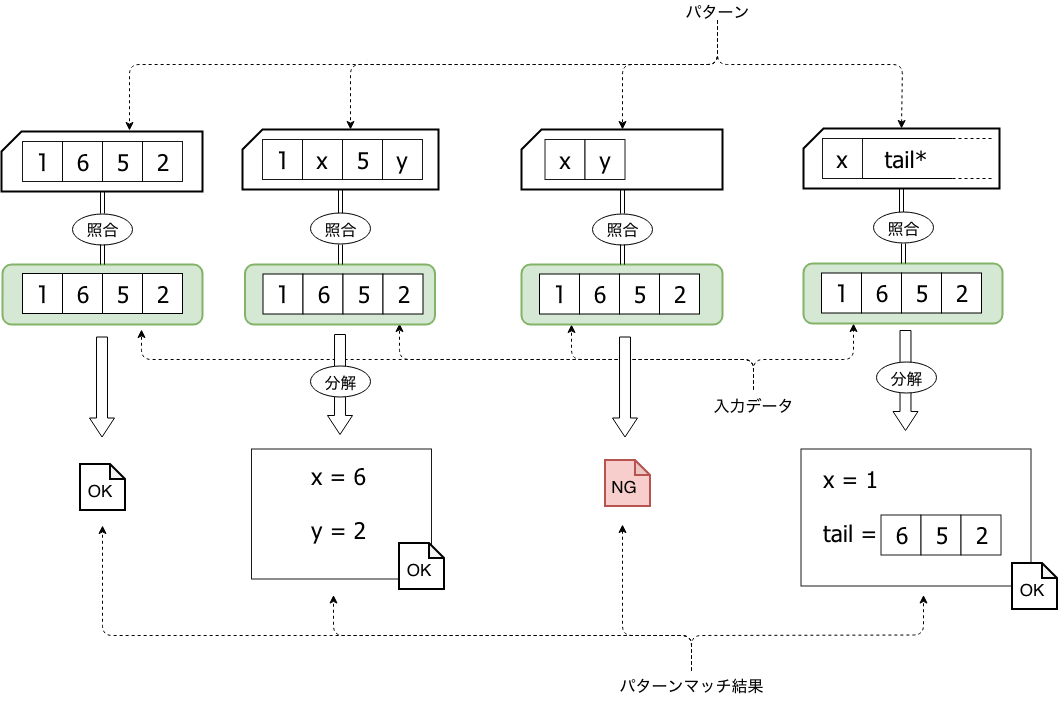
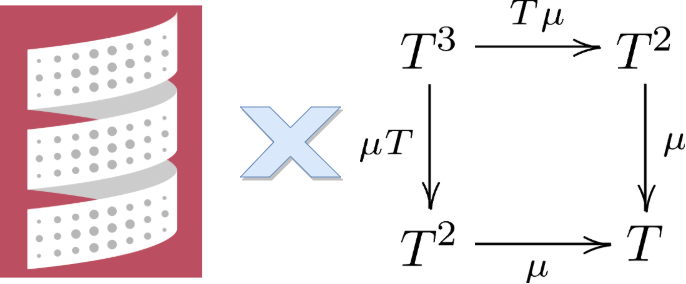最近、圏論とプログラミングという素晴らしい資料を拝読しました。圏論とプログラミング愛に溢れる資料で読んでいて目頭が熱くなりました。そうだよな・・・プログラマにも圏論いるよな・・・

ただ、自分にとって残念だったのは、資料で説明用に選択されたプログラミング言語が「Haskell」だったことです。もちろんHaskellは素晴らしい言語です。ただ、自分にとってHaskellは外国語なのでちょっと理解が難しいのです。そしてこの資料が「Scala」で書かれていたらと夢想せずにはいられなかったのです。

Scalaと言えば昨年末にScala3のリサーチコンパイラのDottyがFeature Completeを宣言しました^1。この宣言で新機能の追加は終了して、あとは2020年末のリリースに向けてひたすら品質を上げていく段階に突入しました。つまり、ようやく次世代のScalaが全貌を現したということです。

ここである考えが脳裏を過りました。もしかしたら「圏論とプログラミング」に出てくるHaskellの記述を「素のScala3」で置き換えられるのではないかと。

本記事ではその疑問を検証してみたいと思います。

TL;DR

  • 圏論とプログラミングに記載されているHaskellの記述をScala3に書き換えてみた
    • Scala3(Dotty)は0.22.0-RC1を利用
    • 外部ライブラリは使わない
      • 標準言語機能と標準ライブラリとコンパイラオプションは利用してもよい
    • メタプログラミングは使わない
    • 書き換えたのは余米田の補題まで
      • それ以降はだれか挑戦してください・・・
  • 結論
    • かなり自然に圏論の概念を記述できるようになった
    • 記述量的にはHaskellに大分近づいたがまだ若干差がある
      • 行数的にはかなり肉薄したが、Scalaは型記述が多いため文字数ではまだ差がある

はじめに

本記事では「圏論とプログラミング」（以降、「元記事」と表記）に記述されているHaskellの記述をScala3(Dotty 0.22.0-RC1)で書き換える検証を行った結果を解説します。

本記事のHaskellのソースコードは基本的に元記事からの引用になります^2。Scala3のコードはなるべくHaskellのソースコードを忠実に再現するようにしていますが、言語の機能や慣習の違いにより様々な差異があることをご了承ください。

基本的には以下のルールで書き換えています。

  • なるべくScala3の新機能^3を用いてスマートに書き換える
    • ただし、0.22.0-RC1のリリース時点で ブログや ドキュメントに利用方法の記載のない機能は本記事では扱わない
  • 外部ライブラリは使わない[^4]
    • 標準言語機能と標準ライブラリのみ使って良い
    • コンパイラオプションは使って良い[^5]
  • メタプログラミングは使わない
    • 本記事では「素のScala3」でどこまでできるかがテーマなので今回は用いないこととする
  • Haskellで用いられている記号の演算子はScalaでは文字のメソッド名に変換する
  • Haskellの型引数は小文字が用いられるが、Scalaでは大文字にする

[^4]: ここで言う新機能とはScala2にはなく、Dotty 0.22.0-RC1に実装されている機能を指しています。まだScala3はリリースされていないので、ここで紹介した機能も変更されたり削除されたりする可能性があります。
[^5]: 元記事のHaskellのコードにもGHCの言語拡張が用いられているので、Scala3でもOKとしました。Scalaでは-Ykind-projectorフラグを利用しています。

Scala3で圏論の概念を実装してみる

それではいよいよScala3で実装してみます。以降のタイトルは元記事と対応しています。元記事の発表スライドメモを並べながら見るとわかりやすいと思います。

型クラスを使った圏の定義

まずは基本的な圏の定義です。行数はHaskellもScala3も3行に収まっていますが、文字数的にはHaskellのほうが少ないようです。

haskell
1
2
3
class Category cat where
    id :: cat a a
    (.) :: cat b c -> cat a b -> cat a c
scala
1
2
3
trait Category[F[_, _]]
  def id[A]: F[A, A]
  def [A, B, C](x: F[B, C]).compose(y: F[A, B]): F[A, C]

Scala 3の解説をすると、まずこのインデント記法を初めて見る方は驚くかもしれません。Scala 3ではHaskellやPythonのようにインデントベースで書けるようになりました。もちろん括弧を用いた記法も可能です。詳細は以下を御覧ください。

また以下の拡張メソッド記法も初見はGo言語っぽいなと思いました。以下のメソッドはF[B,C]型を拡張してcomposeメソッドを追加する構文です。

scala
1
def [A, B, C](x: F[B, C]).compose(y: F[A, B]): F[A, C]

拡張メソッドの詳細は以下を確認してください。

圏の例：クライスリ圏

次にクライスリ圏を定義ですが、その前にモナドを定義する必要があります。モナドの定義は[ここ]から引用させて頂きました。

haskell
1
2
3
4
5
6
7
8
9
10
11
12
class Functor f where
    fmap :: (a -> b) -> f a -> f b

class Functor f => Applicative f where
    pure :: a -> f a
    (<*>) :: f (a -> b) -> f a -> f b

class Applicative m => Monad m where
    (>>=) :: m a -> (a -> m b) -> m b

    return :: a -> m a
    return = pure
scala
1
2
3
4
5
6
7
8
9
10
11
trait Functor[F[_]]
  def [A, B](x: F[A]).map(y: A => B): F[B]

trait Applicative[F[_]] extends Functor[F]
  def [A, B](x: F[A => B]).ap(y: F[A]): F[B]
  def pure[A](f: A): F[A]

  def [A, B](x: F[A]).map(y: A => B): F[B] = ap(pure(y))(x)

trait Monad[F[_]] extends Applicative[F]
  def [A, B](x: F[A]).flatMap(y: A => F[B]): F[B]

Scalaの定義も大分スッキリしていると思います。特徴としてはScala3では継承を用いて実装を行っています。継承を用いずに型制約を実現することもできますが、型が素直なis-a関係にあるときは継承を用いたほうがシンプルになります。また、慣習の違いによりHaskellとScala3では関数名を変えています。Haskellの関数とScalaのメソッドの対応は以下のとおりです。

Haskell Scala3
fmap map
<*> ap
pure pure
>>= flatMap
return pure

準備が整ったのでクライスリ圏の定義を比較してみます。

haskell
1
2
3
4
5
6
7
newtype Kleisli m a b = Kleisli { runKleisli :: a ->  m b}
instance Monad m => Category (Kleisli m) where
    id :: Kleisli m a a
    id = Kleisli pure

    (.) :: Kleisli m b c -> Kleisli m a b -> Kleisli m a c
    f . g = Kleisli (\x -> runKleisli g x >>= runKleisli f)
scala
1
2
3
4
5
6
7
8
9
opaque type Kleisli[F[_], A, B] = A => F[B]
object Kleisli
  def apply[F[_], A, B](x: A => F[B]) = x

given kleisliCategory[F[_]](using m: Monad[F]) as Category[Kleisli[F, *, *]]
  def id[A] = Kleisli(m.pure(_))

  def [A, B, C](x: Kleisli[F, B, C]).compose(y: Kleisli[F, A, B]) =
    Kleisli[F, A, C](k => y(k).flatMap(x))

Scala3では新しく「不透明型エイリアス(Opaque Type Alias)」を用いています。これはHaskellのnewtypeに対応するもので、単一の型のゼロコスト抽象化を提供します。詳細は以下を確認してください。

またScala3では型クラスのインスタンスを定義するためにgiven、using、asという構文が追加されています。これらは従来のimplicit構文をわかりやすくしたものです。詳細は以下を確認してください。

あと、型の部分適用を簡単にするためにKind projector syntax supportを有効にしています。利用した箇所は「Kleisli[F, *, *]」の部分です。詳細は以下を確認してください。

圏の例：レンズ圏

次はレンズ圏の定義です。次はレンズ圏の定義です。定義だけ見ると相当ややこしい感じがします・・・

haskell
1
2
3
4
5
6
7
8
9
10
data Lens a b = Lens (a -> b) (a -> b -> a)

instance Category Lens where
    id :: Lens a a
    id = Lens Prelude.id (const Prelude.id)

    (.) :: Lens b c -> Lens a b -> Lens a c
    Lens g1 s1 . Lens g2 s2 = Lens (g1 Prelude.. g2) s3
        where
            s3 a c = s2 a (s1 (g2 a) c)
scala
1
2
3
4
5
6
7
8
9
10
trait Lens[A, B](val g: A => B, val s: A => B => A)
object Lens
  def apply[A, B](g: A => B, s: A => B => A) = new Lens(g, s){}

given Category[Lens]
  def id[A] = Lens(identity, Function.const(identity))

  def [A, B, C](x: Lens[B, C]).compose(y: Lens[A, B]) =
    val s3: A => C => A = a => c => y.s(a)(x.s(y.g(a))(c))
    Lens(x.g compose y.g, s3)

Scala3では新しくトレイトにパラメータを持てるようになったのでこれを利用しています。またLensを生成しやすくするためにコンパニオンオブジェクトにapplyメソッドを定義しています。Scala3のCreator Applicationsが利用できるかと思ったのですがトレイトには利用できないようです。詳細は以下を確認してください。

関手

ようやく関手まで来ました。ここの関手は圏論の関手です。HaskellのコードはMaybeがHask圏（型と関数の圏）からHask圏への関手になっていることを示していますが、ScalaのコードはMaybeと同等の意味論を持つOptionがScala圏(この名称でいいかは謎)からScala圏への関手になっていることを示しています。

haskell
1
2
3
4
5
6
class (Category c, Category d) => Functor' c d f where
    fmap' :: c a b -> d (f a) (f b)

instance Functor' (->) (->) Maybe where
    fmap' _ Nothing = Nothing
    fmap' f (Just a) = Just (f a)
scala
1
2
3
4
5
6
7
trait Functor_[C[_, _], D[_, _], F[_]](using Category[C], Category[D])
  def fmap[A, B](c: C[A, B]): D[F[A], F[B]]

given Functor_[Function1, Function1, Option]
  def fmap[A, B](f: A => B) = x => x match
    case None => None
    case Some(a) => Some(f(a))

そういえばusingってトレイトに直接書けることを今回気づきました。正直Haskellの定義を見たときにScala3に翻訳するのが難しそうかなって思いましたが、案外簡単にいけました。
また、Functorのgivenインスタンスの実装はHaskellに倣いましたが、以下のようにOptionのmapに委譲もできます。

1
2
given Functor_[Function1, Function1, Option]
  def fmap[A, B](c: A => B) = _.map(c)

自己関手（Endofunctor）

こちらがプログラミングでよく使われる「関手」です。ここでもHaskellをScalaの記述量は大差ないものになっています。

haskell
1
2
3
4
5
6
class Functor f where
    fmap :: (a -> b) -> f a -> f b

instance Functor Maybe where
    fmap _ Nothing = Nothing
    fmap f (Just a) = Just (f a)
scala
1
2
3
4
5
trait Functor[F[_]]
  def [A, B](x: F[A]).map(y: A => B): F[B]

given Functor[Option]
  def [A, B](x: Option[A]).map(y: A => B) = x.map(y)

関手圏と自然変換

ついに関手圏と自然変換までやってきました。そしてここでHaskellとScalaに決定的な差がついてしまいました。

haskell
1
2
3
4
5
6
7
8
newtype f :~> g = NT { unNT :: forall x. f x -> g x }

instance Category (:~>) where
    id :: a :~> a
    id = NT Prelude.id

    (.) :: (b :~> c) -> (a:~> b) -> (a :~> c)
    NT f . NT g = NT (f Prelude.. g)
scala
1
2
3
4
5
6
7
8
9
10
11
trait NT[F[_], G[_]]
  def apply[A](fa: F[A]): G[A]

trait Category2[K[F[_], G[_]]]
  def id[A[_]]: K[A, A]
  def [A[_], B[_], C[_]](x: K[B, C]).compose(y: K[A, B]): K[A, C]

given Category2[NT]
  def id[A[_]] = new NT { def apply[E](fa: A[E]) = fa }
  def [A[_], B[_], C[_]](x: NT[B, C]).compose(y: NT[A, B]) =
    new NT { def apply[X](fa: A[X]) = x(y(fa)) }

まず、Scala3にはHaskellのようなforallがありません。つまり単純にunNTのような関数を定義することはできませんでした。また自然変換(NT)の型引数は2つなので、内部のメソッド(apply)に型引数を追加してunNTっぽい関数を実装しました。こうすることでapplyの型引数Aを外部に晒さずにすみます。

次の問題は自然変換を圏のインスタンスにしようとしたとき、圏(Category)と自然変換(NT)のカインドが異なることです。Categoryのインスタンスになれるのは2つの型引数を持つ1階の型コンストラクタですが、NTは2つの1階の型コンストラクタを引数に持つのでカインドが異なると怒られるのです。こういう場合のためにScala3で追加されたカインドポリモルフィズムが使えるのではと思ったのですが、残念ながら今回のケースでは利用できませんでした。

仕方がないので2つの型コンストラクタを引数にとるCategory2を作成してNTをインスタンスにしてみました・・・

自然変換の例：多相関数

今まで自然変換が多相関数だと言われてもピンと来なかったのですがNTを使ってheadやlengthを実装してみることでようやく腹落ちしました。

まずはheadからです。元記事にはListの定義がなかったので追加しています。

haskell
1
2
3
4
5
6
data List a = Nil' | Cons' a (List a)  -- 元記事になかったので追加

head' :: List :~> Maybe
head' = NT $ \case
    Nil'      -> Nothing
    Cons' a _ -> Just a
scala
1
2
3
4
5
def head: NT[List, Option] = new NT {
  def apply[X](fa: List[X]) = fa match
    case Nil => None
    case a :: _ => Some(a)
}

ScalaではListのメソッドのheadOptionを利用すれば以下のように簡潔に定義できます。

scala
1
2
def head2: NT[List, Option] =
  new NT { def apply[X](fa: List[X]) = fa.headOption }

次にLengthメソッドです。注目すべきはConstです。片側を捨てる関手ですが、こういうときに役に立ちます。

haskell
1
2
3
4
5
newtype Const a b = Const { getConst :: a } -- 元記事になかったので追加
length' :: List :~> Const Int
length' = NT $ \case
    Nil'       -> Const 0
    Cons' _ as -> Const $ 1 + getConst (unNT length' as)
scala
1
2
3
4
5
6
7
8
9
opaque type Const[A, B] = A
object Const
  def apply[A](x: A) = x

def length: NT[List, Const[Int, *]] = new NT {
  def apply[X](fa: List[X]) = fa match
    case Nil => Const(0)
    case _ :: as => Const(1 + length(as))
}

Scala3のコードにも大分なれて来たと思いますが、ここでもKind Projectorを利用してConstにIntを部分適用しています。

米田の補題

ようやく圏論の華もしくは到達点とも言える米田の補題までやってきました。この抽象度の高い概念の記述の際にもScala3はHaskellと同等の記述力を発揮します。

haskell
1
2
3
4
5
newtype Yoneda f a =
    Yoneda { runYoneda :: forall b. (a -> b) -> f b}

instance Functor (Yoneda f) where
    fmap f m = Yoneda (\k -> runYoneda m (k . f))
scala
1
2
3
4
5
6
7
trait Yoneda[F[_], A]
  def apply[B](f: A => B): F[B]

given yonedaFunctor[F[_]] as Functor[Yoneda[F, *]]
  def [A, B](x: Yoneda[F, A]).map(f: A => B) = new Yoneda {
    def apply[C](k: B => C) = x(k compose f)
  }

次にliftYonedaとlowerYonedaです。これもほとんど遜色なく記述できています。

haskell
1
2
3
4
5
liftYoneda :: Functor f => f a -> Yoneda f a
liftYoneda a = Yoneda (\f -> Main.fmap f a) -- 元記事になかったので追加

lowerYoneda :: Yoneda f a -> f a
lowerYoneda (Yoneda f) = f id -- 元記事になかったので追加
scala
1
2
3
4
5
def liftYoneda[F[_], A](fa: F[A])(using Functor[F]): Yoneda[F, A] = new Yoneda {
  def apply[B](f: A => B): F[B] = fa.map(f)
}

def lowerYoneda[F[_], A](y: Yoneda[F, A]): F[A] = y(identity)

余米田の補題(Coyoneda)

最後に余米田の補題です。ここまで来るとFreerモナドの夢を見る一歩手前です。

haskell
1
2
3
4
5
data Coyoneda f a where
    Coyoneda :: (z -> a) -> f z -> Coyoneda f a

instance Functor (Coyoneda f) where
    fmap f (Coyoneda g v) = Coyoneda (f Prelude.. g) v
scala
1
2
3
4
5
6
enum Coyoneda[F[_], A]
  case New[F[_], A, Z](za: Z => A, fz: F[Z]) extends Coyoneda[F, A]

given coyonedaFunctor[F[_]] as Functor[Coyoneda[F, *]]
  def [A, B](x: Coyoneda[F, A]).map(f: A => B) = x match
    case Coyoneda.New(g, v) => Coyoneda.New(f compose g, v)

ここに来てScala3の新機能を利用しました。enumです。Haskellの方でGADTが登場したので満を持してここにenumを持ってきました。enumは代数的データ型を簡単に書ける機能です。詳細は以下を確認してください。

最後にliftCoyonedaとlowerCoyonedaを比較して終わりです。最後は文字数的にも肉薄しています。

haskell
1
2
3
4
5
liftCoyoneda :: f a -> Coyoneda f a
liftCoyoneda = Coyoneda Prelude.id  -- 元記事になかったので追加

lowerCoyoneda :: Functor f =>Coyoneda f a -> f a
lowerCoyoneda (Coyoneda f m) = Main.fmap f m  -- 元記事になかったので追加
scala
1
2
3
4
5
def liftCoyoneda[F[_], A](fa: F[A]) =
  Coyoneda.New(identity[A], fa)

def lowerCoyoneda[F[_]: Functor, A](x: Coyoneda[F, A]) = x match
  case Coyoneda.New(f, m) => m.map(f)

Scala3とHaskellの比較

実際にどれだけのScalaとHaskellの記述量を比較してみました。Haskell側は記述量を揃えるために標準ライブラリで提供されているものも定義しました。

また、Hakellは8個ものGHC言語拡張を利用していました。これもそのままソースコードに記述して行数としてカウントすることにしました。一種のペナルティみたいなものです。

比較結果は以下のとおりです。行数ベースではかなり肉薄していると思います。ただScalaの方が型の記述が多くなるため文字数としてはHaskellが簡潔になります。

言語 文字数（スペース込み） 文字数（スペース無視） 行数
Haskell 2786 2076 113
Scala 3334 2630 112

以下に比較に用いたコンパイル可能なHaskellとScalaのコードを記載します。興味がある方は中を覗いてみてください。

コンパイル可能なHaskellコード
category_haskell.hs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
{-# LANGUAGE InstanceSigs #-}
{-# LANGUAGE MultiParamTypeClasses #-}
{-# LANGUAGE ExistentialQuantification #-}
{-# LANGUAGE RankNTypes #-}
{-# LANGUAGE TypeOperators #-}
{-# LANGUAGE PolyKinds #-}
{-# LANGUAGE LambdaCase #-}
{-# LANGUAGE GADTs #-}

import Prelude hiding (Functor, Applicative, Monad, pure, (>>=))

class Category cat where
    id :: cat a a
    (.) :: cat b c -> cat a b -> cat a c

instance Category (->) where
    id :: (->) a a
    id a = a

    (.) :: (->) b c -> (->) a b -> (->) a c
    f . g = \x -> f (g x)

class Functor f where
    fmap :: (a -> b) -> f a -> f b

class Functor f => Applicative f where
    pure :: a -> f a
    (<*>) :: f (a -> b) -> f a -> f b

class Applicative m => Monad m where
    (>>=) :: m a -> (a -> m b) -> m b

    return :: a -> m a
    return = pure

newtype Kleisli m a b = Kleisli { runKleisli :: a ->  m b}
instance Monad m => Category (Kleisli m) where
    id :: Kleisli m a a
    id = Kleisli pure

    (.) :: Kleisli m b c -> Kleisli m a b -> Kleisli m a c
    f . g = Kleisli (\x -> runKleisli g x >>= runKleisli f)

data Lens a b = Lens (a -> b) (a -> b -> a)

instance Category Lens where
    id :: Lens a a
    id = Lens Prelude.id (const Prelude.id)

    (.) :: Lens b c -> Lens a b -> Lens a c
    Lens g1 s1 . Lens g2 s2 = Lens (g1 Prelude.. g2) s3
        where
            s3 a c = s2 a (s1 (g2 a) c)

class (Category c, Category d) => Functor' c d f where
    fmap' :: c a b -> d (f a) (f b)

instance Functor' (->) (->) Maybe where
    fmap' _ Nothing = Nothing
    fmap' f (Just a) = Just (f a)

instance Functor Maybe where
    fmap _ Nothing = Nothing
    fmap f (Just a) = Just (f a)

newtype f :~> g = NT { unNT :: forall x. f x -> g x }

instance Category (:~>) where
    id :: a :~> a
    id = NT Prelude.id

    (.) :: (b :~> c) -> (a:~> b) -> (a :~> c)
    NT f . NT g = NT (f Prelude.. g)

data List a = Nil' | Cons' a (List a)

head' :: List :~> Maybe
head' = NT $ \case
    Nil'      -> Nothing
    Cons' a _ -> Just a

newtype Const a b = Const { getConst :: a }
length' :: List :~> Const Int
length' = NT $ \case
    Nil'       -> Const 0
    Cons' _ as -> Const $ 1 + getConst (unNT length' as)

newtype Yoneda f a =
    Yoneda { runYoneda :: forall b. (a -> b) -> f b}

instance Functor (Yoneda f) where
    fmap f m = Yoneda (\k -> (runYoneda m) (k Prelude.. f))

liftYoneda :: Functor f => f a -> Yoneda f a
liftYoneda a = Yoneda (\f -> Main.fmap f a)

lowerYoneda :: Yoneda f a -> f a
lowerYoneda (Yoneda f) = f Prelude.id

data Coyoneda f a where
    Coyoneda :: (z -> a) -> f z -> Coyoneda f a

instance Functor (Coyoneda f) where
    fmap f (Coyoneda g v) = Coyoneda (f Prelude.. g) v

liftCoyoneda :: f a -> Coyoneda f a
liftCoyoneda = Coyoneda Prelude.id

lowerCoyoneda :: Functor f => Coyoneda f a -> f a
lowerCoyoneda (Coyoneda f m) = Main.fmap f m

main = do
    putStrLn "Hello Category Theory!"
コンパイル可能なScala3コード
category_scala.scala
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
object CategoryTheoryExampleDefs
  trait Category[F[_, _]]
    def id[A]: F[A, A]
    def [A, B, C](x: F[B, C]).compose(y: F[A, B]): F[A, C]

  given Category[Function1]
    def id[A] = x => x
    def [A, B, C](x: Function1[B, C]).compose(y: Function1[A, B]) = a =>x(y(a))

  trait Functor[F[_]]
    def [A, B](x: F[A]).map(y: A => B): F[B]

  trait Applicative[F[_]] extends Functor[F]
    def [A, B](x: F[A => B]).ap(y: F[A]): F[B]
    def pure[A](f: A): F[A]

    def [A, B](x: F[A]).map(y: A => B): F[B] = ap(pure(y))(x)

  trait Monad[F[_]] extends Applicative[F]
    def [A, B](x: F[A]).flatMap(y: A => F[B]): F[B]

  opaque type Kleisli[F[_], A, B] = A => F[B]
  object Kleisli
    def apply[F[_], A, B](x: A => F[B]) = x

  given kleisliCategory[F[_]](using m: Monad[F]) as Category[Kleisli[F, *, *]]
    def id[A] = Kleisli(m.pure(_))

    def [A, B, C](x: Kleisli[F, B, C]).compose(y: Kleisli[F, A, B]) =
      Kleisli[F, A, C](k => y(k).flatMap(x))

  trait Lens[A, B](val g: A => B, val s: A => B => A)
  object Lens
    def apply[A, B](g: A => B, s: A => B => A) = new Lens(g, s){}

  given Category[Lens]
    def id[A] = Lens(identity, Function.const(identity))

    def [A, B, C](x: Lens[B, C]).compose(y: Lens[A, B]) =
      val s3: A => C => A = a => c => y.s(a)(x.s(y.g(a))(c))
      Lens(x.g compose y.g, s3)

  trait Functor_[C[_, _], D[_, _], F[_]](using Category[C], Category[D])
    def fmap[A, B](c: C[A, B]): D[F[A], F[B]]

  given Functor_[Function1, Function1, Option]
    def fmap[A, B](f: A => B) = x => x match
      case None => None
      case Some(a) => Some(f(a))

  given Functor[Option]
    def [A, B](x: Option[A]).map(y: A => B) = x.map(y)

  trait NT[F[_], G[_]]
    def apply[A](fa: F[A]): G[A]

  trait Category2[K[F[_], G[_]]]
    def id[A[_]]: K[A, A]
    def [A[_], B[_], C[_]](x: K[B, C]).compose(y: K[A, B]): K[A, C]

  given Category2[NT]
    def id[A[_]] = new NT { def apply[E](fa: A[E]) = fa }
    def [A[_], B[_], C[_]](x: NT[B, C]).compose(y: NT[A, B]) =
      new NT { def apply[X](fa: A[X]) = x(y(fa)) }

  def head: NT[List, Option] = new NT {
    def apply[X](fa: List[X]) = fa match
      case Nil => None
      case a :: _ => Some(a)
  }

  opaque type Const[A, B] = A
  object Const
    def apply[A](x: A) = x

  def length: NT[List, Const[Int, *]] = new NT {
    def apply[X](fa: List[X]) = fa match
      case Nil => Const(0)
      case _ :: as => Const(1 + length(as))
  }

  trait Yoneda[F[_], A]
    def apply[B](f: A => B): F[B]

  given yonedaFunctor[F[_]] as Functor[Yoneda[F, *]]
    def [A, B](x: Yoneda[F, A]).map(f: A => B): Yoneda[F, B] = new Yoneda {
      def apply[C](k: B => C) = x(k compose f)
    }

  def liftYoneda[F[_], A](fa: F[A])(using Functor[F]): Yoneda[F, A] = new Yoneda {
    def apply[B](f: A => B): F[B] = fa.map(f)
  }

  def lowerYoneda[F[_], A](y: Yoneda[F, A]): F[A] = y(identity)

  enum Coyoneda[F[_], A]
    case New[F[_], A, Z](za: Z => A, fz: F[Z]) extends Coyoneda[F, A]

  given coyonedaFunctor[F[_]] as Functor[Coyoneda[F, *]]
    def [A, B](x: Coyoneda[F, A]).map(f: A => B) = x match
      case Coyoneda.New(g, v) => Coyoneda.New(f compose g, v)

  def liftCoyoneda[F[_], A](fa: F[A]) =
    Coyoneda.New(identity[A], fa)

  def lowerCoyoneda[F[_]: Functor, A](x: Coyoneda[F, A]) = x match
    case Coyoneda.New(f, m) => m.map(f)

@main def example: Unit =
   import CategoryTheoryExampleDefs.{_, given}
    println("Hello Category Theory")

HaskellとScala3の開発環境

HaskellとScala 3の開発環境にはVisual Studio Codeを使いました。どちらも文法エラーですぐに赤くなるし、マウスオーバーで型がすぐに分かるので非常に助かりました。Language Server Protocolは偉大です。環境構築は以下を参照しました。

まとめ

圏論とプログラミングに記載されているHaskellコードを以下の条件でScala3に書き換えてみました。
  • Scala3(Dotty)は0.22.0-RC1を利用
    • 外部ライブラリは使わない
      • 標準言語機能と標準ライブラリとコンパイラオプションは利用してもよい
    • メタプログラミングは使わない
  • 余米田の補題まで書き換えてみた
    • それ以降はだれか挑戦してください・・・

結論としては、Scala3でかなり自然に圏論の概念を記述できるようになったように感じました。記述量的にも大分Haskellに近づいたように思います。この一年近くはScala3のimplicit周りの文法がめちゃくちゃ変わってどうなるか心配だったのですが、なんとなくいい感じの文法に仕上がってきたのではないかと思います（個人の感想です）。あとはラムダ関数がジェネリクスに対応してくれるとかなり嬉しいですね^6。

本記事がScala3と圏論に興味がある方の一助になれば幸いです。

おまけ

いつの間にか圏論と学びをめぐる往復書簡というものが始まっていました。数学ガールの圏論版が出て欲しいなぁ・・・

参考文献

article.related_posts

最近の記事

リンク

カテゴリ

アーカイブ

タグ

AWS14
AdventCalendar6
Algorithm1
Azure1
Blog1
Book5
CDK1
CategoryTheory2
Cats1
Certification4
Cloud2
Compiler1
Container3
Diet1
Dotty3
Environment1
ErgoDash2
Event11
Exam1
FizzBuzz1
Flourish2
GCP3
Game1
Git2
Go3
Hexo6
IaC1
Interpreter1
Jupyter4
Keras1
Keyboard7
Keymap1
M11
MLOps1
Mac1
MachineLearning5
MakerFaire1
Mind1
Minikube1
OGP1
Qiita1
ReView1
Ruby6
Rust6
SEO1
Scala8
Serverless1
Snowflake1
StepFunctions1
TensorFlow1
TypeScript1
UI/UX1
WFH1
Web5
WebAnalytics1
gRPC1
html51
k8s3
npm4
oEmbed2
pulumi1
Your browser is out-of-date!

Update your browser to view this website correctly.&npsb;Update my browser now

×

×